Retour à la page précédente

Commun

M. GUITARD

 M.ROTY M. THIERIOT

Comment a-t-on compté à travers les âges ?

La page a été mise à jour le 

Prérequis

Savoir compter, additionner, soustraire, multiplier, diviser... et utiliser les puissances !

 

Introduction

Un des objectifs de l'option MPI est de pouvoir communiquer avec un ordinateur en utilisant son propre langage : le langage binaire encore appelé langage numérique. Pour bien comprendre ce langage, il est utile de prendre du recul par rapport à notre manière de compter et de découvrir que les civilisations qui nous ont précédés ont développé des manière de compter parfois fort différentes de la nôtre !

Quoiqu'il en soit, il est nécessaire de définir quelques notions communes à toutes les numérations. Cela nous permettra ainsi de les différencier...

Chiffres et nombres


Dans toute numération, il faut distinguer chiffres et nombres.

  • Un nombre est le résultat du comptage d'un ensemble d'objets, d'animaux, de personnes ...

  • Pour écrire un nombre, on peut utiliser un ou plusieurs chiffres.

Une année comporte douze mois : douze (12) est un nombre comportant deux chiffres (1 et 2).
Les jours de la semaine sont au nombre de 7 : Ce nombre s'écrit avec un seul chiffre (7).
 

 Numération d'addition et de position
 
- Dans la  numération d'addition, lorsqu'un nombre est représenté par plusieurs chiffres, la valeur du nombre est égale à la somme des chiffres quelque soit leur position
Si nous utilisions la numération additive, 77 vaudrait 14  !
Et 58 aurait la même valeur que 85 soit 13 !

- Dans la numération de position, la position des chiffres les uns par rapport aux autres à une grande importance, un même chiffre n'a pas la même valeur suivant sa position. 
Quand nous écrivons 33, nous savons que l'un des trois vaut 3 et l'autre vaut 30 !

 

Point de départ

Quelques repères historiques pour découvrir d'autres numérations

Rédacteur JMR + CG

Retour au sommaire général

D'après une idée consultable sur le site académique : http://www.ac-rennes.fr/pedagogie/scphys/accueil.htm
 

-

Retour en haut de la page

Quelques repères...

La numération de position décimale: notre manière actuelle de compter.

On a pris l'habitude de compter en "paquets". La numération moderne regroupe les éléments à dénombrer en "paquets" de dix. On dit qu'on utilise la "base dix".

Exemple :  2 582 = 2 x 103 + 5 x 102 + 8 x 101 + 2 x 100       ( NB : il faut se rappeler que 100 =1 )
Bien remarquer que le premier chiffre 2 vaut 2000 alors que le dernier ne vaut que 2 !

 

1) Quels sont les chiffres du système de numération décimale utilisé aujourd'hui?

2) Combien de nombres peut-on écrire avec ces chiffres?

3) Notre système de numération est il de position ou d'addition? Justifie.

4) Décomposer le nombre 37 804 en une addition à l'aide des puissances de dix (comme dans l'exemple ci-dessus)..

Fais vérifier tes réponses...

Repères historiques

Pour mieux comprendre cette façon de compter, et pour bien se rendre compte que ce n'est pas la seule manière valable de compter, revenons quelques milliers d'années en arrière ...

Asie   Moyen-Orient / Égypte       Europe   Amérique

 
  - 30 000   Entailles numériques sur des os ou de la corne.  

 

Mésopotamie

Usage des calculi (jetons d'argile).

calculi.gif (1670 octets)

   - 8 000  
 

 

Mésopotamie

 Création des chiffres cunéiformes pour compter les animaux, les hommes et pour chiffrer les récoltes.
cuneif.gif (1339 octets)

   - 3 300  
 

 

Égypte

Usage de la numération additive à base dix.

num_egyp1.gif (1473 octets)

   - 2 000 (env.)  
 

 

Babylone

Première numération de position (base 60).

cun_1_10.gif (1055 octets)

   - 1 800  
 
Invention des chiffres en Chine.  
  - 1 300  
 

 
  - 400  

Numération grecque

 Système hybride, ni purement additif, ni vraiment de position.

  

 


Première invention du zéro:
cun_1_10_0.gif (1242 octets)

   - 300 (env.)  

Numération romaine

num_rom1.gif (1555 octets)

  
Numération de position à base dix en Inde : Invention du zéro.

Créations de dix chiffres correspondants chacun à un symbole différent.

  
  4ème siècle  
 

 
  5ème siècle  
 

Numération maya de position

Numération à base 20 utilisant le zéro.

 
  10ème siècle  

Chiffres arrivant en Espagne : Partis de l'Inde, ils ont étés modifiés au Moyen-Orient et au Maghreb.

  

 
  12ème siècle   Arrivée du zéro en Europe.

Numération de position à base dix

  
        ...        
Numération décimale : Manière actuelle de compter ...

Numération binaire (base de 2) : Langage utilisé par les ...

Numération hexadécimale (base de 16) très utilisée en ...

   de nos jours   ... C'est une numération de position.

... ordinateurs. (numération de position)

... informatique. (numération de position)

 

Retour en haut de la page

 

-

Retour en haut de la page

La numération égyptienne : 
une numération d'addition

 

La numération égyptienne utilisait les hiéroglyphes ci-contre. Leurs symboles évoquent chacun un ordre de grandeur.
  • un bâton évoque l'unité,
  • une anse de panier: il contient environ 10 objets,
  • une rouleau de papyrus: on peut y écrire environ 100 hiéroglyphes,
  • une fleur de lotus: on les trouve par milliers,
  • un doigt montrant le ciel nocturne: on y voit près de 10 000 étoiles,
  • un têtard: on en trouve de l'ordre de 100 000 au bord du Nil après la ponte,
  • un dieu agenouillé supportant le ciel: le dieu est éternel et 1 million d'années est synonyme d'éternité).

On additionne les valeurs de tous les signes utilisés pour écrire le nombre.
2964.gif (2487 octets)
On peut vérifier que ce nombre est 2964.

Les chiffres employés


num_egyp.gif (2100 octets)

1) Recopie les chiffres du système de numération égyptien.

2) Traduis les nombres 2006 et 30240.

3) Ce système de numération est il de position ou d'addition? Prouve le en écrivant un nombre de plusieurs manières.

4) Traduis le nombre 99. Pourquoi la numération de position est-elle un progrès par rapport à la numération d'addition ?

 

Fais vérifier tes réponses...

Retour en haut de la page

 

-

Retour en haut de la page

La numération romaine :
transition entre la numération d'addition et de position

 

Jusqu'au MOYEN-AGE, la numération romaine permettait d'écrire les neufs premiers chiffres ainsi :

rom_1-9.gif (1612 octets)

Il s'agissait encore d'une numération d'addition comme on le voit à travers l'écriture du chiffre quatre ou du chiffre neuf. 
Ci-contre les différents signes employés sachant qu'une barre au-dessus correspond à ( x 103 ). Exemple :

vaut cent mille

 


Ce n'est qu'à partir du MOYEN-AGE qu'on a écrit les chiffres romains en utilisant des différences telles que IV (pour quatre), IX (pour neuf), XC (pour quatre-vingt dix)... La position des chiffres a donc pris à ce moment une réelle importance !

 

 

Signes employés

  1) Recopiesr les signes employés par le système de numération romaine.

2) Écris les nombres 99, 1948 et 2001 en numération romaine d'avant puis d'après le moyen-age. 
Quelle est la numération la plus avantageuse ? Pourquoi ?


3) Traduis les nombres ci-dessous en numération actuelle :

 a)   ex_rom2.gif (1404 octets)                   b)   ex_rom1.gif (1448 octets)

 

Fais vérifier tes réponses...

Retour en haut de la page

 

-

Retour en haut de la page

La numération maya :
Une numération de position en base 20

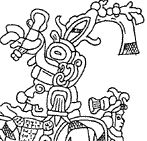
stele_m.gif (4910 octets)

La base vingt
Les Mayas ont adapté leur système de numération à leur calendrier. Leur numération est à base vingt, comme leurs mois qui comptaient vingt jours.

Ci-dessous les chiffres de 1 à 19 ainsi que le chiffre zéro :

num_maya.gif (2531 octets)

Et après ?
Le nombre 20 s'écrit alors avec deux symboles alignés verticalement (voir ci-contre).

20_maya.gif (1202 octets)

Les Mayas écrivaient leurs nombres de bas en haut.

 

1) Recopie les signes  utilisés pour écrire les chiffres de 0 à 19 ?

2) Que représentent les trois nombres ci-dessous écrits en base vingt ?

400

8000

combien?

3) Traduis les nombres 55, 100, 531. 

4) Traduis le nombre 20. Essaie maintenant de l'écrire sans le chiffre 0 : Pourquoi le zéro a-t-il été inventé avec l'apparition de la numération de position ?

Fais vérifier tes réponses...

 
L'influence du calendrier.

Le calendrier maya était établi ainsi :

  • le mois (uinal) comptait vingt jours
  • les années (tun) comptaient 360 jours (on rattrapait les jours manquants en fin d'année)
  • 1 katun comportait 20 années (tun)
  • 1 baktun comportait 20 katun

La numération maya était utilisée pour le calendrier.  Il est donc possible de convertir en jours une date écrite en maya (voir exemple ci-contre).
Attention cependant, une année ne comporte que 360 jours il est donc nécessaire de multiplier par 360 au lieu de 400 !


cal_num.gif (1927 octets)

Le nombre ci-dessus correspond à 729 942 jours : combien cela fait en année ?

Remarque : Les dates mayas partent de 3113 avant notre ère ; cette date semble être la point de départ du Monde pour les Mayas.

 

Retour en haut de la page

 

-

Retour en haut de la page

La numération babylonienne :
une numération de position en base 60

 

Il y a 4000 ans, en Mésopotamie est apparu le premier système de numération. On a retrouvé des jetons en terre cuite dont les valeurs (1, 10, 60, 600, 3600 et 36000)  permettaient de réaliser tous les nombres entiers.
La numération écrite est ensuite apparue avec l'écriture, vers 3300 av JC. Elle permettait de gérer les troupeaux, les récoltes, les hommes, les superficies des terres.

 

Cette numération additive, sumérienne à l'origine, utilisait des petits clous, des grands clous, des chevrons. La confusion possible entre grands clous et petits clous la fit évoluer vers une numération de position.

 

Lorsque la numération de position fut inventée, la nécessité du zéro se fit sentir. Il fallut tout de même un millénaire et demi pour parvenir à la numération de position à base soixante avec zéro. Cette numération ne comporte que trois signes: le un, le dix et le zéro.

 

Les nombres, en Mésopotamie, étaient écrits sur des plaques d'argile fraîche. Les scribes utilisaient une tige de roseau taillée appelée calame. Par séchage au soleil, on obtient ainsi des tablettes dont la conservation est excellente. On en a retrouvé de grandes quantités.

calame.gif (1323 octets)calame

calculi.gif (1670 octets)

Les formes utilisées étaient le petit cône, la sphère, le grand cône, le cône perforé et la sphère perforée.

 

cuneif.gif (1339 octets)

           cun_1_10_0.gif (1242 octets)

cun_nbr1.gif (1800 octets)
Le nombre à trois chiffres ci-dessus (base 60) se traduit en numération décimale par :
5 x 602 + 3 x 601 + 31 x 600 = 18 211

 

cun_nbr2.gif (2067 octets)

1) Recopie les 3 signes utilisés par le système babylonien de position.

2)Traduis en numération décimale le  nombre ci-dessus.

3) Écris en numération babylonienne le nombre 155.

4) Dans tous les systèmes décrits jusqu'ici on remarque l'omniprésence du nombre 10 ou de ses multiples. Comment expliques tu cela?

5) Écris le nombre 7200 en numération babylonienne. Quel inconvénient présentait l'écriture de ce nombre avant que le zéro ne soit inventé?

L'héritage des babyloniens.
L'astronome grec Hipparque introduisit en Grèce (2ème siècle av JC), la division du cercle en 360 degrés, chaque degré étant divisé en 60 minutes et chaque minute en 60 secondes. Nous avons conservé ce vestige de la base soixante des Babyloniens, par l'intermédiaire d'Hipparque.

 

Retour en haut de la page

 

-

Retour en haut de la page

Des numérations pour l'ère numérique !

 

Rappel : Deux façons de compter avec ses dix doigts

Avec la  méthode additive Avec la numération de position
Aucune convention nécessaire, cela nous paraît évident : un doigts levé vaut un, une main (avec les doigts levés) vaut cinq, et les deux mains valent dix... On convient alors de dire qu'un doigt baissé compte zéro, mais chaque doigt levé représente le chiffre un et compte une valeur qui dépend de sa position.

doigt_num.gif (1528 octets)

On utilise alors la base deux.
Pour montrer la valeur 37, on peut présenter trois fois de suite ses mains avec les doigts levés, ce qui signifie 3 fois 10, puis on montre les deux mains avec sept doigts levés.

Que faudrait-il faire pour indiquer le nombre 245 selon la méthode ci-dessus ?

Quelle est la valeur indiquée avec les conventions ci-dessous ?

doigt_n1.gif (1147 octets)

Quel est le plus grand nombre qui puisse être représenté par les doigts des deux mains ?

 

Applications : Utilité du binaire (ou base de deux)

En électronique (courants électriques), ou en photonique (lumière), il n'existe que deux états : On est donc amené à utiliser la base deux.
Tension          fleche1.gif (873 octets)   1 Lumière          fleche1.gif (873 octets)   1
Pas de tensionfleche1.gif (873 octets)  0 Pas de lumièrefleche1.gif (873 octets)  0

Pourquoi un enregistrement sur cédérom ou sur disque dur ne permet-il pas d'utiliser autre chose que la base deux ?


C'est aussi la numération idéale de l'informatique.

Un ordinateur ne sait utiliser que des informations binaires que nous noterons 0 (ZERO) et 1 (UN). On a donc que DEUX états. Le niveau 0 correspond à une absence de tension alors que le niveau 1 correspond à une tension supérieure à la tension de basculement.

Cette information binaire est stockée dans une case mémoire appelée bit ( contraction de binary digit).
Si on utilise en même temps deux cases binaires, on peut maintenant avoir QUATRE états différents (00,01,10,11).  

Quels sont les huit états différents que l'on peut obtenir avec trois cases binaires utilisées en même temps ?
Combien d'états différents aura-t-on avec quatre cases binaires ?

 

L'octet (ou byte) est composé de huit cases binaires.

Il peut prendre alors 256 valeurs de :                 

0 0 0 0 0 0 0 0 soit 0 (en décimal)

à

1 1 1 1 1 1 1 1 soit 255

Même question : Généraliser au cas de l'octet.        

 

Pour aller plus loin : La base de seize ou hexadécimal

Observons ces captures d'écran :

- dans un éditeur d'image (en l'occurrence Paint Shop Pro)

    

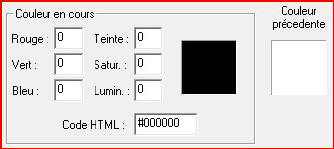
- dans un éditeur HTML (en l'occurrence FrontPage)

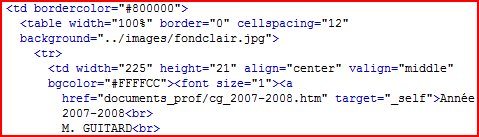
Les logiciels utilisent des codes hexadécimaux (on le voit ici identifier les couleurs) : Quel est l'intérêt ?

Que pensez-vous de l'écriture du nombre 1 million en base deux ? Pour répondre, identifie le nombre binaire (a, b, c ou d) ayant la valeur la plus proche de 1 million (1 000 000 en base dix) :

a) 1 0000 0000 0000 0000 0000
b) 1 0000 0000 0000 0000		  c) 1 0000 0000 0000
 d) 1 0000 0000

Bref, l'écriture est un peu longue !

Or on peut remarquer qu'un demi-octet va de zéro à quinze. On peut donc utiliser la base seize pour remplacer un demi-octet.

0 1 2 3 ... 9 A B C D E F
zéro un deux trois ... neuf dix onze douze treize quatorze quinze

L'octet valant 255, il devient donc en base seize : FF

1 1 1 1 1 1 1 1

F

 F

Ceci permet d'écrire simplement les adresses des mémoires de l'ordinateur ou par exemple les codes des 16 millions de couleurs utilisées en informatique.

Traduire FFFFFF en décimal puis en binaire. Conclure.

On reconstitue les couleurs en informatique à partir du rouge, du vert et du bleu. Sachant que chaque couleur est codée par un octet, combien de couleurs peut-on ainsi reconstituer ?

  En fait, chaque couple de chiffres code une couleur, dans l'ordre : rouge, vert, bleu.
Ainsi le blanc est codé par FF FF FF et le noir est codé par 00 00 00.

 

Retour en haut de la page