Histoire de la numération

|
Extrait de "mpi_html" consultable sur le site académique :http://www.ac-rennes.fr/pedagogie/scphys/accueil.htm |
|
Histoire de la numération |
|
Sujet : Comment l'Humanité s'est-elle doté d'un système de numération qui permet de dénombrer et de calculer ? A qui doit-on notre système de numération ?
Remarque : Ce chapitre correspond à l'alinéa du programme "Quelques éléments d'histoire de la numération".
Plan :
| 1 : Définitions | |
|
Chiffres et nombres :
Une année comporte douze mois: douze (12) est un nombre
comportant deux chiffres (1 et 2). Base : |
Questions :
1) Combien de chiffres comporte le système de numération décimale utilisé aujourd'hui? 2) Le zéro est-il utile pour l'écriture des nombres? Si oui, quels inconvénients présenterait sa non utilisation? 3) Décomposer le nombre 37 804 en une addition de cinq parties à l'aide des puissances de dix. |
| 2 : Deux grands types de numération | |||
|
Numération additive |
Numération de position |
||
La numération égyptienne
utilisait les hiéroglyphes ci-contre. Leurs symboles évoquent chacun
un ordre de grandeur.
On additionne les valeurs de tous les signes utilisés pour écrire
le nombre. |
Les chiffres
|
Un exemple actuel: la numération
décimale moderne utilisant les chiffres arabes. La valeur représentée par un chiffre dépend de sa position. 3 344 = 3 x 103 + 3 x 102 + 4 x 101 + 4 x 100 C'est pourquoi on parle de numération de position. On fait ainsi l'économie de l'écriture de nombreux signes. |
Les chiffres
|
| Questions | |||
| 1) Écrire les nombres 10275 et
2000. 2) Le zéro est-il nécessaire dans ce type de numération. 3) Faire une phrase pour donner le principe d'une numération additive. 4) Quelle base utilise la numération égyptienne? D'après vous, pourquoi cette base a-t-elle été souvent choisie dans les numérations inventée par l'homme? |
5) Dire simplement, à partir de l'écriture d'un même nombre dans les deux numérations ci-dessus, une raison pour laquelle les numérations de position sont un progrès par rapport aux numérations additives. | ||
|
Autres exemples |
|||
| Numération romaine | Numération savante chinoise | ||
La numération romaine permettait d'écrire
les neufs premiers chiffres ainsi: On remarque l'écriture du chiffre quatre et celle du chiffre neuf.
Ce n'est qu'au MOYEN-AGE qu'on a écrit les chiffres romains en
utilisant des différences telles que IX (neuf), XC (quatre-vingt
dix)... |
Signes employés:
ainsi de suite sachant que un trait sur le symbole multiplie sa valeur par 103. |
Cette numération à base dix
était utilisée pour les mathématiques. Elle comporte neuf chiffres,
le zéro étant indiqué par une case vide (espace). Il existe deux
sortes de chiffres (voir ci-contre) selon le rang. Ainsi, 1987 s'écrit et 2026 s'écrit On pourrait reprocher à ce système de numération un
risque d'erreur, si l'espace est oublié. L'alternance des deux types de
chiffres évite cette ambiguïté. Toutefois, le risque existe si deux
zéros se suivent, mais il est impossible de ne pas remarquer le double
espace.
Ces abaques ont ensuite disparu. |
Colonne 1:
chiffres de rangs impairs, utilisés pour les unités,
les centaines, ... Colonne 2: chiffres de rangs pairs, utilisés pour les dizaines, les milliers, ...
Le boulier permet d'afficher les nombres selon cette même logique. |
| Questions | |||
| 6) Écrire les nombres 1948 et
2001 en numération romaine. 7) Traduire les nombres ci-dessous en numération actuelle. |
8) Lire les nombres suivants : 9) Écrire en numération savante chinoise, les nombres ci-dessous : 3962, 640, 64 et 6400. |
||
| 3 : La numération Maya : la base vingt | ||||||
|
La base vingt
Les Mayas écrivaient leurs nombres de bas en haut :
|
Questions 1) Combien de signes sont utilisés pour écrire les chiffres de 0 à
19?
|
|||||
L'influence
du calendrier
La numération maya étant utilisée pour le calendrier, il advint que le nombre représentant une date correspondait exactement aux subdivisions du calendrier. Ainsi, le chiffre d'ordre 3, (ici 7) était à multiplier par 360 au lieu de 400:
Cette date peut donc être calculée en jours. |
3) Quel serait le nombre de jours
correspondant à la date ci-contre (à gauche), si on utilisait
réellement la base vingt?
4) Quel est le nombre de jours correspondant à cette date en tenant
compte des subdivisions du calendrier maya? |
|||||
| Un exemple d'écriture maya
(glyphe)
|
||||||
| 4 : La numération mésopotamienne : la base soixante | |
| Il y a 4000 ans, en Mésopotamie est apparu
le premier système de numération. On a retrouvé des jetons en terre
cuite dont les valeurs (1, 10, 60, 600, 3600 et 36000)
permettaient de réaliser tous les nombres entiers. La numération écrite est ensuite apparue avec l'écriture, vers 3300 av JC. Elle permettait de gérer les troupeaux, les récoltes, les hommes, les superficies des terres. |
|
| Cette numération additive, sumérienne à l'origine, utilisait des petits clous, des grands clous, des chevrons. La confusion possible entre grands clous et petits clous la fit évoluer vers une numération de position. |
|
| Lorsque la numération de position fut inventée, la nécessité du zéro se fit sentir. Il fallut tout de même un millénaire et demi pour parvenir à la numération de position à base soixante avec zéro. Cette numération ne comporte que trois signes: le un, le dix et le zéro. |
|
Les nombres, en Mésopotamie, étaient
écrits sur des plaques d'argile fraîche. Les scribes utilisaient une
tige de roseau taillée appelée calame. Par séchage
au soleil, on obtient ainsi des tablettes dont la conservation est
excellente. On en a retrouvé de grandes quantités. calame calame |
|
| Questions | |
| 1) Traduire en numération décimale le
nombre ci-contre.
2) Écrire en numération babylonienne le nombre 155. 3) Écrire le nombre 72000 en numération babylonienne. Quel inconvénient présentait l'écriture de ce nombre avant que le zéro ne soit inventé? |
|
| Pour aller plus loin | |
| L'héritage des babyloniens. L'astronome grec Hipparque introduisit en Grèce (2ème siècle av JC), la division du cercle en 360 degrés, chaque degré étant divisé en 60 minutes et chaque minute en 60 secondes. Nous avons conservé ce vestige de la base soixante des Babyloniens, par l'intermédiaire d'Hipparque. |
|
| 5 : La démarche vers la numération moderne | |
| Au départ, l'Homme du fait de l'élevage et
de l'agriculture, fut conduit à dénombrer ses animaux et ses
récoltes. Il trouva des moyens simples, tels que des encoches sur des bâtons ou des os ou bien encore des noeuds sur des cordes. |
|
|
|
Ensuite, il imagina des calculs à l'aide de jetons d'argile de valeurs différentes. |
| Ces jetons furent ensuite représentés par
des symboles sur des plaquettes d'argile. C'est l'invention des
chiffres. Les symboles s'additionnent. Les moyens d'écriture sont simples. Un roseau coupé laisse son empreinte dans l'argile fraîche. |
|
 |
On passe ensuite à une numération de
position qui permet d'écrire des nombres aussi grand que l'on veut. Enfin, le zéro est inventé, permettant une numération sans ambiguïté. |
| Les chiffres deviennent des symboles individuels et non un assemblage de signes, grâce à la numération indienne. Cette dernière évolue progressivement en passant par le Moyen-Orient, le Maghreb et l'Espagne maure pour arriver aux chiffres actuels. |
|
| 6 : Historique de la numération | ||||
| Date | Asie | Amérique | Europe | Moyen-Orient / Egypte |
| - 30 000 | Entailles numériques sur des os ou de la corne. | |||
| - 8 000 | Mésopotamie: Usage des calculi
(jetons d'argile ayant une valeur attribuée et permettant de
représenter un nombre). |
|||
| - 3 300 | Mésopotamie: Création des
chiffres cunéiformes pour compter les animaux, les hommes et pour
chiffrer les récoltes. |
|||
| - 2 000 (env) | Égypte : Usage de la numération
additive à base dix.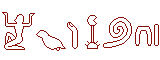 |
|||
| - 1 800 | Babylone: Première numération de position (base 60).
|
|||
| - 1 300 | Invention des chiffres en Chine. | |||
| - 400 | Système de numération grecque. Système hybride, ni purement additif, ni vraiment de position. | |||
| - 300 (env) | Système de numération romaine. |
|
||
| 4ème siècle | Numération de position à base
dix en Inde. Invention du zéro. Créations de dix chiffres correspondants chacun à un symbole différent. |
|||
| 5ème siècle | Numération maya de position. Invention du zéro. | |||
| 10ème siècle | Chiffres arrivant en Espagne. Partis de l'Inde, ils ont étés modifiés au Moyen-Orient et au Maghreb. | |||
| 12ème siècle | Arrivée du zéro en Europe. | |||
| Questions | ||||
| 1) Faire la liste des lieux et des dates où fut inventé le zéro? | ||||
| 2) Combien de temps s'est écoulé entre l'invention de nos chiffres en Inde et leur arrivée en Europe? | ||||
| 3) Que serait-il probablement arrivé si l'Homme possédait six doigts sur chacune des deux mains? | ||||
| 7 : Un système de numération en 3D | ||
|
Dans le boulier, chaque tige porte deux boules qui valent cinq (en haut) et cinq boules qui valent un (en bas).
|
Questions
|
|
| Les boules rapprochées du centre sont seules
comptabilisées.
Ci-contre la valeur affichée est : 1 x 5 + 2 x 1 = 7. |
|
2) Faire un schéma représentant l'affichage du chiffre neuf puis du chiffre zéro. |
| Le boulier fonctionne comme un système de
numération de position à base dix. Le chiffre indiqué à droite correspond aux unités. |
|
3) Quel est le nombre affiché ci-contre? |
|
Le boulier est très pratique pour réaliser des
additions ou des soustractions. |
4) Réaliser les schémas du boulier affichant les nombres 386 puis 153. Enfin, en utilisant uniquement ces schémas (sans calcul) afficher le résultat de la somme 386 + 153 sur un autre schéma de boulier. | |
| 8 : Des numérations pour l'ére numérique ! | |||||||||||||||||||||||||||||||||||||||||
|
Deux façons de compter sur ses dix doigts |
|||||||||||||||||||||||||||||||||||||||||
|
La méthode additive |
Avec la numération de position |
||||||||||||||||||||||||||||||||||||||||
| Pour montrer la valeur 37, on
peut présenter trois fois de suite ses mains avec les doigts levés, ce
qui signifie 3 fois 10, puis on montre les deux mains avec sept doigts
levés. |
On convient alors de dire qu'un
doigt baissé compte zéro, mais chaque doigt levé représente le
chiffre un et compte une valeur qui dépend de sa position. On utilise alors la base deux. On utilise alors la base deux. |
||||||||||||||||||||||||||||||||||||||||
| Questions | |||||||||||||||||||||||||||||||||||||||||
| 1) Que faudrait-il faire pour indiquer le nombre 245 selon la méthode ci-dessus ? |
2) Quelle est la valeur indiquée avec les conventions ci-dessous ?
3) Quel est le plus grand nombre qui puisse être représenté par les doigts des deux mains? |
||||||||||||||||||||||||||||||||||||||||
|
Applications : Les numérations de l'électronique et de la photonique |
|||||||||||||||||||||||||||||||||||||||||
En électronique (courants
électriques), ou en photonique (lumière), il n'existe que deux états:
On est donc amené à utiliser la base deux.
à
C'est la numération idéale de l'informatique. |
Questions
|
||||||||||||||||||||||||||||||||||||||||
| Toutefois, pour les grands
nombres, l'écriture est un peu longue.
|
2) Quel est le nombre binaire
(base deux) ci-dessous le plus proche de 1 million (1 000 000 en base
dix)? a) 1 0000 0000 0000 0000 0000; b) 1 0000 0000 0000 0000; c) 1 0000 0000 0000; d) 1 0000 0000. 3) Que pensez-vous de l'écriture du nombre 1 million en base deux ? |
||||||||||||||||||||||||||||||||||||||||
| Un demi-octet, on peut le
vérifier, va de zéro à quinze. On peut donc utiliser la base seize pour remplacer un demi-octet.
L'octet valant 255, il devient donc en base seize :
Ceci permet d'écrire simplement les adresses des mémoires de l'ordinateur ou par exemple les codes des 16 millions de couleurs utilisées en informatique. |
4) Traduire FFFFFF en décimal puis en
binaire. Conclure.
5) On reconstitue les couleurs en informatique à partir du rouge, du vert et du bleu. Sachant que chaque couleur est codée par un octet, combien de couleurs peut-on ainsi reconstituer ? Remarque : |
||||||||||||||||||||||||||||||||||||||||